Cracking Case Studies: Conquer Your CBSE Class 10 Maths Exam (2023-24 Session)
With the CBSE Class 10 board exams just around the corner (March 11th, 2024!), many students feel a surge of anxiety, especially when it comes to case-based questions in Maths. The lengthy descriptions can be daunting, making them seem complex. But fear not! Case-based questions are actually a great opportunity to showcase your problem-solving skills, provided your foundational concepts are strong.
This blog post is your one-stop guide to mastering case studies in your upcoming Maths exam. The CBSE board format incorporates 3 case study questions, each worth a total of 4 marks (broken down as 1+1+2). To help you ace these questions, I've compiled a list of practice problems directly from the official CBSE sample papers. By familiarizing yourself with these case studies before the big day, you'll be well-equipped to tackle them with confidence. So, let's dive in and conquer those case studies!
| Class | 10 |
| Board | CBSE |
| Subject | Mathematics (Standard) |
| Exam Date | 11/03/2024 |
| Content-Type | Important Case Based Questions |
| Session | 2023-24 |
| Official Website | https://www.cbse.gov.in/ |
Also See: 🎯 Class 10 Maths (Standard) Topper's Answer Sheet (2023) ✨
Q. No. 1) Manpreet Kaur is the national record holder for women in the shot-put discipline. Her throw of 18.86m at the Asian Grand Prix in 2017 is the maximum distance for an Indian female athlete. Keeping her as a role model, Sanjitha is determined to earn gold in the Olympics one day.

Initially, her throw reached 7.56m only. Being an athlete in school, she regularly practiced both in the mornings and in the evenings and was able to improve the distance by 9cm every week.
During the special camp for 15 days, she started with 40 throws and every day kept increasing the number of throws by 12 to achieve this remarkable progress.
(i) How many throws Sanjitha practiced on 11th day of the camp?
(ii) What would be Sanjitha’s throw distance at the end of 6 weeks?
(or)
When will she be able to achieve a throw of 11.16 m?
(iii) How many throws did she do during the entire camp of 15 days?
Ans. (i) Number of throws during camp. a = 40; d = 12
𝑡11 = 𝑎 + 10𝑑
= 40 + 10 × 12
= 160 𝑡ℎ𝑟𝑜𝑤𝑠
(ii) a = 7.56 m; d = 9cm = 0.09 m
n = 6 weeks
tn = a + (n-1)d
= 7.56 + 6(0.09)
= 7.56 + 0.54
Sanjitha’s throw distance at the end of 6 weeks = 8.1 m
(or)
a = 7.56 m; d = 9cm = 0.09 m
tn =11.16 m
tn = a + (n-1) d
11.16 = 7.56 + (n-1) (0.09)
3.6 = (n-1) (0.09)
n-1 = 3.6/0.09 = 40
n = 41
Sanjitha’s will be able to throw 11.16 m in 41 weeks.
(iii) a = 40; d = 12; n = 15
Sn = n/2[2a + (n-1) d]
Sn =15/2[2(40) + (15-1) (12)]
= 15/2[80 + 168]
= 15/2[248] =1860 throws
Q. No. 2) Tharunya was thrilled to know that the football tournament is fixed with a monthly timeframe from 20th July to 20th August 2023 and for the first time in the FIFA Women’s World Cup’s history, two nations host in 10 venues. Her father felt that the game can be better understood if the position of players is represented as points on a coordinate plane.
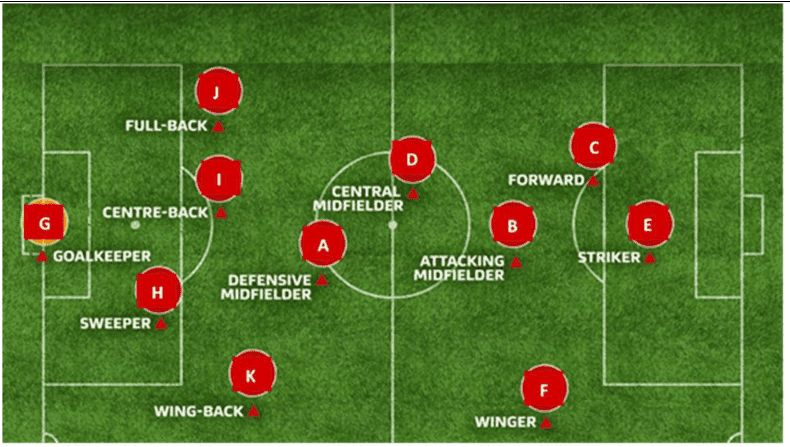
(i) At an instance, the midfielders and forward formed a parallelogram. Find the position of the central midfielder (D) if the position of other players who formed the parallelogram are:- A(1,2), B(4,3) and C(6,6)
(ii) Check if the Goal keeper G(-3,5), Sweeper H(3,1) and Wing-back K(0,3) fall on a same straight line.
[or]
Check if the Full-back J(5,-3) and centre-back I(-4,6) are equidistant from forward C(0,1) and if C is the mid-point of IJ.
(iii) If Defensive midfielder A(1,4), Attacking midfielder B(2,-3) and Striker E(a,b) lie on the same straight line and B is equidistant from A and E, find the position of E.
Ans. (i) Let D be (a,b), then
Mid point of AC = Midpoint of BD
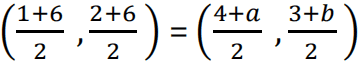
4 + a = 7 and 3+ b = 8
a = 3 and b = 5
Central midfielder is at (3,5)
ii.
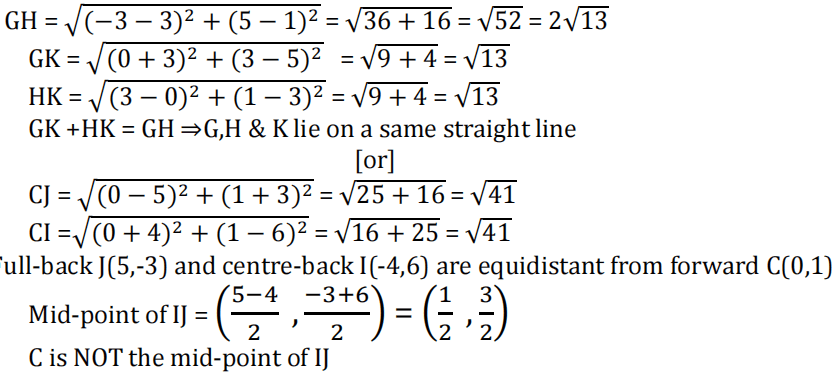
iii. A, B and E lie on the same straight line and B is equidistant from A and E
⇒ B is the mid-point of AE
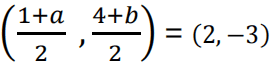
1 + 𝑎 = 4 ; a = 3.
4+b = -6; b = -10
E is (3,-10)
Q. No. 3) One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°.
When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
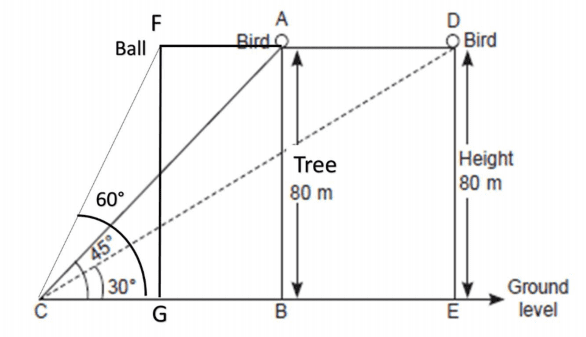
(i) At what distance from the foot of the tree was he observing the bird sitting on the tree?
(ii) How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball?
(iii) What is the speed of the bird in m/min if it had flown 20(√3 + 1) m?
Ans. i. tan 45° = 80/CE
⇒ 1/√3 = 80/CE
⇒ CE = 80√3
Distance the bird flew = AD = BE = CE-CB = 80√3 – 80 = 80(√3 -1) m
(or)
tan 60° = 80/CG
⇒ √3 = 80/CG
⇒ CG = 80/√3
Distance the ball travelled after hitting the tree =FA=GB = CB -CG
GB = 80 - 80/√3 = 80 (1- 1/√3) m
iii. Speed of the bird = distance/time = 20(√3 + 1)/2 m/sec = 10(√3 + 1)m/sec = 10(√3 + 1) x 60 m/min = 600(√3 + 1) m/min
Q. No. 4) An interior designer, Sana, hired two painters, Manan and Bhima to make paintings for her buildings. Both painters were asked to make 50 different paintings each.
The prices quoted by both the painters are given below:
- Manan asked for Rs 6000 for the first painting, and an increment of Rs 200 for each following painting.
- Bhima asked for Rs 4000 for the first painting, and an increment of Rs 400 for each following painting.
(i) How much money did Manan get for his 25th painting? Show your work.
(ii) How much money did Bhima get in all? Show your work.
(iii) If both Manan and Bhima make paintings at the same pace, find the first painting for which Bhima will get more money than Manan. Show your steps.
OR
(iii) Sana's friend, Aarti hired Manan and Bhima to make paintings for her at the same rates as for Sana. Aarti had both painters make the same number of paintings, and paid them the exact same amount in total.
How many paintings did Aarti get each painter to make? Show your work.
Ans. i. Notes that the amounts Manan is paid for each painting forms an AP.
Takes a = 6000, d = 200 and n = 25 to find the amount as
6000 + (25 - 1)200 = Rs 10800.
ii. Finds the total amount earned by Bhima as follows:
S50 = 50/2 [2(4000) + (50 - 1)(400)]
Solves the above expression to find the total amount as Rs 6,90,000.
iii. Frames equation as follows:
6000 + (n - 1)200 = 4000 + (n - 1)400
Solves the above equation to find the value of n as 11.
Writes that, since they both earn the same amount for the 11th painting, as Bhima's increment is more, Bhima gets more money than Manan for the 12th painting.
OR
Assumes that the number of paintings required is n.
Frames equation as follows:
Sn(Manan) = Sn(Bhima)
=> 𝑛/2 [2(6000) + (n -1)200] = 𝑛/2 [2(4000) + (n -1)400]
Solves the equation from step 1 to find n as 21.
Q. No. 5) In the game of archery, a bow is used to shoot arrows at a target board. The player stands far away from the board and aims the arrow so that it hits the board.
One such board, which is divided into 4 concentric circular sections, is drawn on a coordinate grid as shown. Each section carries different points as shown in the figure. If an arrow lands on the boundary, the inner section points are awarded.
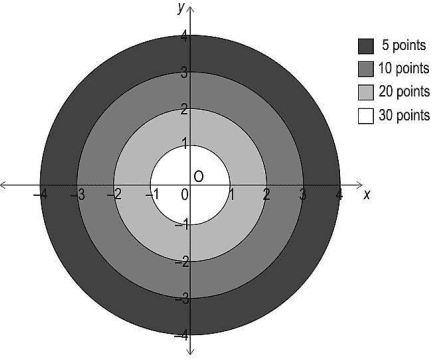
(i) After shooting two arrows, Rohan scored 25 points.
Write one set of coordinates for each arrow that landed on the target.
(ii) If one player's arrow lands on (2, 2.5), how many points will be awarded to the player? Show your work.
(iii) One of Rohan’s arrow landed on (1.2, 1.6). He wants his second arrow to land on the line joining the origin and first arrow such that he gets 10 points for it.
Find one possible pair of coordinates of the second arrow's landing mark. Show your work.
OR
(iii) An arrow landed on the boundary and is worth 20 points. The coordinates of the landing mark were of the form (m, -m).
Find all such coordinates. Show your steps.
Ans. i. Writes two pairs of possible coordinates such that Rohan scored 20 and 5 points for them. For examples, (1.5, 0) and (3.5, 0).
ii. Finds the distance of (2, 2.5) from (0, 0) as:
√(4 + 6.25) = √10.25 units
Hence, concludes that 5 points will be awarded.
iii. Finds the distance of (1.2, 1.6) from the origin as:
√{(1.2)2 + (1.6)2} = 2 units
Assumes that the second arrow lands on the boundary mark and writes that the ratio in which the first arrow divides the origin and the second arrow's landing mark is the ratio of their radii = 2:1.
Assumes the coordinates of the second arrow's landing mark as (x, y) and uses section formula to write:
(2𝑥+0/3 , 2𝑦+0/3) = (1.2, 1.6)
Solves the above equation to find the values of the coordinates of the second arrow's landing mark as (1.8, 2.4).
OR
Identifies the distance between the origin and the coordinate (m, -m) as 2 units and uses the distance formula to write the equation as:
m2 + (-m)2 = 22
Simplifies the above equation as 2m2 = 4.
Solves the above equation to get y as √2 and (-√2).
Finds the coordinates as (√2, -√2) and (-√2, √2)
Q. No. 6) A drone, is an aircraft without any human pilot and is controlled by a remote-control device. Its various applications include policing, surveillance, photography, precision agriculture, forest fire monitoring, river monitoring and so on.
David used an advanced drone with high resolution camera during an expedition in a forest region which could fly upto 100 m height above the ground level. David rode on an open jeep to go deeper into the forest. The initial position of drone with respect to the open jeep on which David was riding is shown below.
David’s jeep started moving to enter the forest at an average speed of 10 m/s. He Simultaneously started flying the drone in the same direction as that of the jeep.
(i) David reached near one of the tallest trees in the forest. He stopped the drone at a horizontal distance of 5√3 m from the top of the tree and at a vertical distance of 65 m below its maximum vertical range.
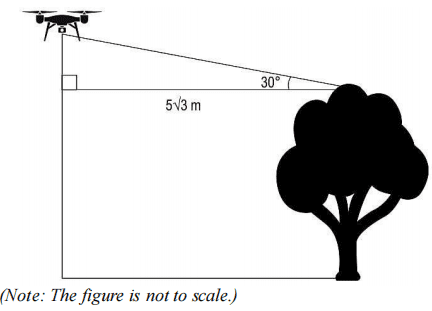
If the angle of elevation of the drone from the top of the tree was 30°, find the height of the tree. Show your work.
(ii) The drone was flying at a height of 30√3 metres at a constant speed in the horizontal direction when it spotted a zebra near a pond, right below the drone.
The drone travelled for 30 metres from there and it could see the zebra, at the same place, at an angle of depression of θ from it.
Draw a diagram to represent this situation and find θ. Show you work.
(iii) After 2 minutes of starting the expedition both the drone and the jeep stopped at the same moment so that the drone can capture some images. The position of the drone and the jeep when they stopped is as shown below.
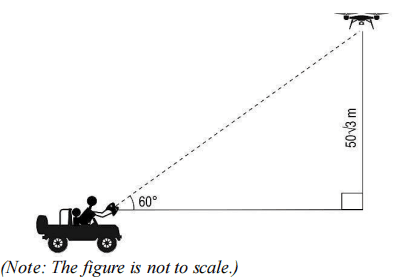
Find the average speed of the drone in m/s rounded off upto 2 decimal places. Show your work.
OR
(iii) At some point during the expedition, David kept the drone stationary for some time to capture the images of a tiger. The angle of depression from the drone to the tiger changed from 30° to 45° in 3 seconds as shown below.
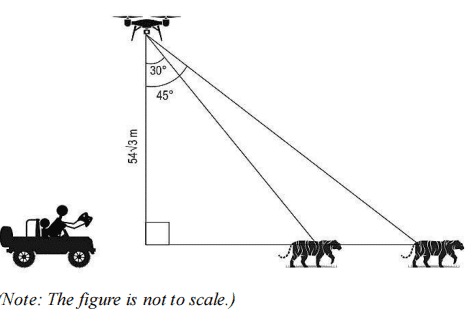
What was the average speed of the tiger during that time? Show your work.
(Note: Take √3 as 1.73.)
Ans. Assumes the vertical distance between the top of the tree and the drone to be h and finds h as:
h = 5√3 × tan 30° = 5√3 × 1/√3 = 5 m
Finds the height of the tree as 100 - 65 - 5 = 30 m
ii.
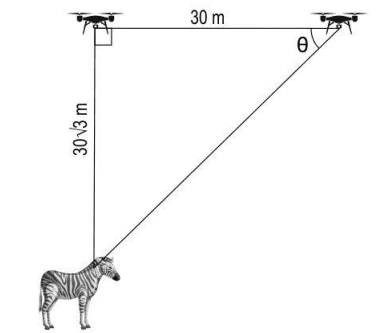
Finds the value of θ as:
tan θ = 30√3/30 = √3
Thus finds the value of θ as 60°
iii. Assumes the horizontal distance between the remote and the drone as x and finds its value as:
x = 50√3/tan60° = 50 m
Finds the distance covered by the jeep in 2 mins as:
10 × 120 = 1200 m
Finds the horizontal distance covered by the drone before it stopped as:
1200 + 50 = 1250 m
Finds the speed of the drone as:
1250/120 = 10.42 m/s
OR
Assumes the horizontal distance between the drone and the tiger to be x when the angle of depression was 30° and finds the value of x as:
x = 54√3 × tan 30° = 54√3 × 1/√3 = 54 m
Assumes the horizontal distance between the drone and the tiger after 3 seconds as y and finds the value of y as:
y = 54√3 × tan 45° = 54√3 m
Finds the distance covered by the tiger in 3 seconds as:
54√3 - 54 = 39.42 m
Finds the average speed of the tiger during that time as:
39.42/3 = 13.14 m/s
Q. No. 7) Shown below is the trophy shield Akshi received on winning an international Table tennis tournament.
The trophy is made of a glass sector DOC supported by identical wooden right triangles
∆ DAO and ∆ COB. Also, AO = 7 cm and AO : DA = 1 ∶ √3 (Use √3 = 1.73)
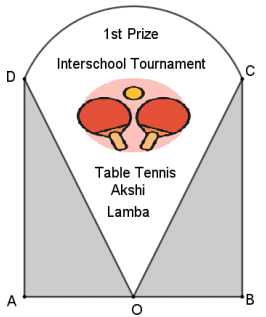
Based on the given information, answer the following questions:
(i) Find ∠𝐷𝑂𝐶
(ii) Find the area of the wooden triangles
(iii) Find the area of the shape formed by the glass portion
OR
If Akshi wants to decorate the boundary of the glass portion with glitter tape, then find the length of the tape she needs.
Ans. (i) Let ∠𝐷𝑂𝐴 = 𝜃, then tan 𝜃 =𝐴𝐷/𝐴𝑂 = √3/1 ⟹ 𝜃 = 60°
∠𝐷𝑂𝐴 = ∠𝐶𝑂𝐵 = 60°
∠𝐷𝑂𝐶 = 180° − (60° + 60°) = 60°
(ii) Area of two wooden triangles = 2 × 1/2 × 7 × 7√3 = 84.77 𝑐𝑚2
(iii) 𝐴𝑂/𝐷𝑂 = cos 60° ⟹ 7/𝐷𝑂 = 1/2
⟹ 𝐷𝑂 = 14 𝑐𝑚
Area of sector 𝐷𝑂𝐶 = 60/360 × 𝜋 × 142 = 102.67 𝑐𝑚2
OR
𝐴𝑂/𝐷𝑂 = cos 60° ⟹ 7/𝐷𝑂 = 1/2
⟹ 𝐷𝑂 = 14 𝑐𝑚
Length of tape required = 2 × 14 + 60/360 × 2 × 𝜋 × 14 = 42.67 cm
Q. No. 8) A school auditorium has to be constructed with a capacity of 2000 people. The chairs in the auditorium are arranged in a concave shape facing towards the stage in such a way that each succeeding row has 5 seats more than the previous one.

(i) If the first row has 15 seats, then how many seats will be there in 12th row?
(ii) If there are 15 rows in the auditorium, then how many seats will be there in the middle row?
(iii) If total 1875 guests were there in the auditorium for a particular event, then how many rows will be needed to make all of them sit?
OR
If total 1250 guests were there in the auditorium for a particular event, then how many rows will be left blank out of total 30 rows?
Ans. (i) 𝑎 = 15, 𝑑 = 5
𝑎12 = 15 + 11×5 = 70
(ii) 𝑛 = 15
Middle row = 8th row
𝑎8 = 15 + 7 × 5 = 50
(iii) 1875 = 𝑛/2 [2 × 15 + (𝑛 − 1) × 5]
⟹ 𝑛2 + 5𝑛 − 750 = 0
⟹ (𝑛 + 30)(𝑛 − 25) = 0 ⟹ 𝑛 = 25
∴ Total number of rows required = 25
OR
1250 = 𝑛/2 [2×15 +(𝑛 − 1) × 5]
⟹ 𝑛2 + 5𝑛 − 500 = 0
(𝑛 + 25)(𝑛 − 20) = 0 ⟹ 𝑛 = 20
∴ Number of rows left = 30 − 20 = 10
Q. No. 9) The students of Class X of a secondary school have been allotted a rectangular plot of land for their gardening activity. Saplings are being planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to row seeds of the flowering plant on the remaining area of the plot.
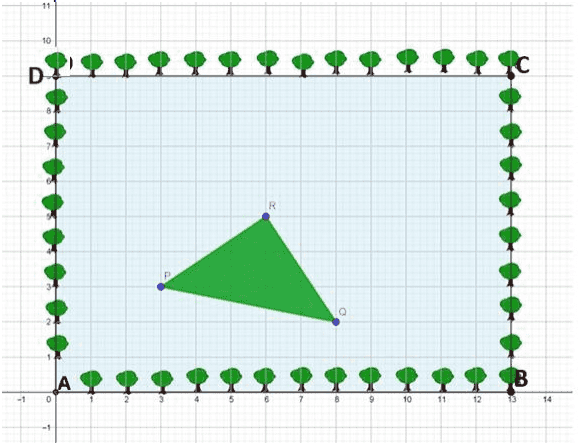
(i) If a tree is to be planted exactly in the middle of the triangle PQR ie. at the centroid of ∆PQR to give shed to the people sitting in the lawn, then find the coordinates of the point where the tree should be planted.
(ii) What type of triangle is formed by the grassy lawn?
(iii) Find the area of the plot in which the students have to row the seeds.
OR
If a special flowering plant has to be planted at a point which divides the line joining the points C and Q in the ratio 2:3, then find the coordinates of the point where this plant will be planted
Ans. (i) 𝑃(3,3), 𝑄(8,2), 𝑅(6,5)
Coordinates of required point are ( 3+8+6/3, 3+2+5/3) = ( 17/3 , 10/3 )
(ii) 𝑃𝑅 = 𝑄𝑅 = √13
𝑃𝑄 = √26
𝑃𝑄2 = 𝑃𝑅2 + 𝑄𝑅2
∴ ∆ 𝑃𝑄𝑅 is an isosceles right triangle
(iii) Area of the plot to row seeds = 13 × 9 − 1/2 × √13 × √13 = 110.5 𝑚
OR
Coordinates of required point are ( 2×8 + 3 ×13/2+3, 2×2+3×9/2+3) = (11, 31/5 )

7.56 + 6(0.09) the answer you provided in question 1 subdivision 2was wrong please correct th